Работа по теме «Объем и площадь цилиндра, пирамиды, конуса и шара» выполнена по предмету «Геометрия» с использованием компьютерной программы POWERPOINT. Актуальность данной темы объясняется изучением геометрических тел, объемов и площадей их поверхностей в 11 классе. Данная работа содержит материал по следующим вопросам: цилиндр; объем цилиндра; площадь цилиндра; пирамида, правильная пирамида и усеченная пирамида; объем пирамиды; конус; площадь поверхности конуса; объем конуса; шар; объем шара; примеры решенных задач; задачи для самостоятельного решения.
Данная работа содержит научный материал. Работа оформлена красочно, использованы рисунки, модели геометрических тел. Различные приемы анимации при демонстрации работы подчеркивают главные моменты работы. Применение эффектов анимации, построение графических элементов слайдов облегчает восприятие изучаемого материала. Презентация включает слайды, которые разработаны с использованием MicrosoftPowerPoint, и довольно успешно может сопровождать лекции преподавателя и быть хорошим помощником при самостоятельной работе учащихся.
Скачать:
Предварительный просмотр:
https://accounts.google.com
Подписи к слайдам:
Рассмотрим правильную пирамиду P А 1 A 2 …A n (см. Рис. 12). Сначала докажем, что все боковые ребра этой пирамиды равны. Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота пирамиды РО, а другим – радиус описанной около основания окружности (например, боковое ребро P А 1 – гипотенуза треугольника О P А 1 , в котором ОР = h , ОА 1 = R . По теореме Пифагора любое боковое ребро равно, поэтому: P А 1 = P А 2 = … = P А n Рис. 12 .
Мы доказали, что боковые ребра правильной пирамиды P А 1 A 2 …A n равны друг другу, поэтому боковые грани – равнобедренные треугольники. Основания этих треугольников также равны друг другу, так как А 1 A 2 …A n – правильный многоугольник. Следовательно, боковые грани равны по третьему признаку равенства треугольников, что и требовалось доказать. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. На рисунке 12 отрезок PE – одна из апофем. Ясно, что все апофемы правильной пирамиды равны друг другу. Докажем теорему о площади боковой поверхности правильной пирамиды. Теорема Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. Доказательство Боковые грани правильной пирамиды равные равнобедренные треугольники, основания которых - стороны основания пирамиды, а высоты равны апофеме. Площадь боковой поверхности пирамиды S равна сумме произведений сторон основания на половину апофемы d . Вынося множитель 1/2d за скобки, получим в скобках сумму сторон основания пирамиды, т. е. его периметр. Теорема доказана.
Усеченная пирамида Возьмем произвольную пирамиду P А 1 A 2 …A n и проведем секущую плоскость β , параллельную плоскости основания пирамиды и пересекающую боковые ребра в точках B 1 , B 2 , … , B n (рис. 13). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n - угольники и А 1 A 2 … A n , B 1 B 2 … B n (нижнее и верхнее основания), расположенные в параллельных плоскостях, и четырехугольники A 1 A 2 B 2 B 1 , A 2 A 3 B 3 B 2 , … , A n A 1 B 1 B n (боковые грани), называется усеченной пирамидой. Отрезки A 1 B 1 ,A 2 B 2 ,…,A n B n называются боковыми ребрами усеченной пирамиды. Усеченную пирамиду с основаниями А 1 A 2 … A n и B 1 B 2 … B n обозначают так: А 1 A 2 … A n B 1 B 2 … B n . Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды. На рисунке 13 отрезок CH является высотой усеченной пирамиды. Рис. 13
Докажем, что боковые грани усеченной пирамиды – трапеции. Рассмотрим, например, боковую грань A 1 A 2 B 2 B 1 (см. рис. 13). Стороны A 1 A 2 и B 1 B 2 параллельны, поскольку принадлежат прямым, по которым плоскость PA 1 A 2 пересекается с параллельными плоскостями и β . Две другие стороны и этой грани не параллельны – их продолжения пересекаются в точке P . Поэтому данная грань – трапеция. Аналогично можно доказать, что и остальные боковые грани – трапеции. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами. Площадью боковой поверхности усеченной пирамиды называется сумма площадей ее боковых граней.
Объём пирамиды Рис. 14.1 Обозначим через x абсциссу точки пересечения этой плоскости с осью O x а через S(x) – площадь сечения. Выразим S(x) через S , h и x . Заметим, что треугольники A 1 B 1 C 1 и ABC подобны. В самом деле, A 1 B 1 ||AB , поэтому Δ O A 1 B 1 подобен Δ O AB . Следовательно, A 1 B 1 /AB = OA 1 /OA . Теорема Объем пирамиды равен одной трети произведения площади основания на высоту. Доказательство Сначала докажем теорему для треугольной пирамиды, а затем – для произвольной пирамиды. 1. Рассмотрим треугольную пирамиду OABC с объемом V , площадью основания S и высотой h . Проведем ось O x (Рис. 14.1 где OM – высота пирамиды) и рассмотрим сечение A 1 B 1 C 1 пирамиды плоскостью, перпендику - лярной к оси O x и, значит, параллельной плоскости основания.
Прямоугольные треугольники ОА 1 М 1 и ОАМ также подобны (они имеют общий острый угол с вершиной О). Поэтому. Таким образом, . Аналогично доказывается, что и, . Итак, треугольники А 1 В 1 С 1 и АВС подобны с коэффициентом подобия. Следовательно, или. Применяя теперь основную формулу для вычисления объемов тел при a = 0 , b = 0 , получаем
2. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S . Такую пирамиду можно разбить на треугольные пирамиды с общей высотой h (на рисунке 14.2 показано разбиение для пятиугольной пирамиды). Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель 1/3 h , получим в скобках сумму площадей оснований треугольных пирамид, т. е. Площадь основания S исходной пирамиды. Таким образом, объем исходной пирамиды равен 1/3 Sh . Теорема доказана. Рис. 14. 2
Следствие Объем V усеченной пирамиды, высота которой равна h , а площади оснований равны S и S 1 , вычисляются по формуле:
Конус Рассмотрим окружность L с центром O и прямую OP перпендикулярную к плоскости от этой окружности. Через точку P и каждую точку окружности проведем прямую. Поверхность, образованная этими прямыми, называется конической поверхностью (рис. 15), а сами прямые – образующими конической поверхности. Точка P называется вершиной, а прямая OP – осью конической поверхности. Тело, ограниченное конической поверхностью и кругом с границей называется конусом (Рис. 16). Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключенные между вершиной и основанием, – образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Ось конической поверхности называется осью конуса, а ее отрезок, заключенный между вершиной и основанием, – высотой конуса. Отметим, что все образующие конуса равны друг другу. Основание конуса Боковая поверхность конуса Образующие конуса Вершина конуса Ось конуса Рис. 15 Рис. 16
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке 17 изображен конус, полученный вращением прямоугольного треугольника ABC вокруг катета AB . При этом боковая поверхность конуса образуется вращением гипотенузы AC , а основание – вращением катета BC . Рассмотрим сечение конуса различными плоскостями. Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг с центром O 1 расположенным на оси конуса. Радиус r этого круга равен PO 1 /PO · r , где r – радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников POM и PO 1 M 1 Рис. 17
Площадь поверхности конуса Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав ее по одной из образующих (Рис. 18.1 и 18.2). Разверткой боковой поверхности конуса является круговой сектор (см. Рис. 18.2), радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса. За площадь боковой поверхности конуса принимается площадь ее развертки. Выразим площадь S бок. боковой поверхности конуса через его образующую l и радиус основания r . Площадь кругового сектора – развертки боковой поверхности конус (см. Рис. 18.2) – равна l 2 / 360 · , где – градусная мера дуги ABA ´ , поэтому S бок. = l 2 /360 · . (1) Выразим через l и r . Так как длина дуги ABA ´ равна 2 r (длине окружности основания конуса), то 2 r = l /180 · , откуда = 360 r/ l . Подставив это выражение в формулу (1), получим S бок. = rl . (2) Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления площади S кон. полной поверхности конуса получается формула S кон. = r (l + r) . Рис. 18. 2 Рис. 18.1
Объём конуса Обозначим радиус этого круга через R 1 , а площадь сечения через S(x) , где x – абсцисса точки M 1 . Из подобия прямоугольных треугольников OM 1 A 1 и OMA следует, что OM 1 /OM = R 1 /R или x/h = R 1 /R , откуда R 1 = R/x ·h . Так как S(x) = R 1 2 , то S(x) = R 2 /h 2 ·x 2 . Применяя основную формулу для вычисления объемов тел при a = 0 , b = h , получаем. Площадь основания конуса равна R 2 , поэтому V = 1/3 Sh . Теорема доказана. Теорема Объем конуса равен одной трети произведения площади основания на высоту. Доказательство Рассмотрим конус с объемом V , радиусом основания R высотой h и вершиной в точке O . Введем ось O x так, как показано на рисунке 19 (x – ось конуса). Произвольное сечение конуса плоскостью, перпендикулярной к оси O x является кругом с центром в точке M 1 пересечения этой плоскости с осью O x . Рис. 19
Следствие Объем V усеченного конуса, высота которого равна h , а площади оснований равны S и S 1 , вычисляется по формуле:
Шар Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (Рис. 20). Данная точка называется центром сферы (точка O на рисунке 20), а данное расстояние – радиус сферы. Радиус сферы часто обозначают латинской буквой R . Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Очевидно, диаметр сферы равен 2R . Отметим, что сфера может быть получена вращением полуокружности вокруг ее диаметра (Рис. 21). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Очевидно, шар радиуса R с центром O содержит все точки пространства, которые расположены от точки O на расстоянии, не превышающем R (включая и точку O), и не содержит других точек. Рис. 2 0 Рис. 2 1
Объём шара Обозначим радиус этого круга через r , а его площадь через S(x) где x – абсцисса точки M . Выразим S(x) через x и R . Из прямоугольного треугольника OMC находим. Так как S(x) = r 2 , то S(x) = (R 2 – x 2) . Заметим, что эта формула верна для любого положения точки M на диаметре AB т. е. для всех x , удовлетворяющих условию: - R ≤ x ≤ R . Применяя основную формулу для вычисления объемов тел при a = - R , b = R , получаем Теорема доказана. Теорема Объем шара радиуса R равен 4/3R 3 . Доказательство Рассмотрим шар радиуса R с центром в точке O и выберем ось O x произвольным образом (Рис. 22). Сечение шара плоскостью, перпендикулярной к оси O x и проходящей через точку M этой оси, является кругом с центром в точке M . Рис. 2 2
Список используемой литературы / [ Л.С. Анатасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия, 10 – 11: учеб. для общеобразоват. учреждений М.: Просвещение, 2011. – 256 с. АтанасянЛ.С., Бутузов В.Ф., Кадомцев СБ., Позняк Э.Г., Юдина И.И. Геометрия. 7-9 классы: Учебник для общеобразовательных учреждений. М.: Просвещение, 2011.
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Муниципальное образовательное учреждение «Средняя общеобразовательная школа №12» на тему: Объём и площадь Тимофеева Галина Александровна МОУ «СОШ № 12» г. Щекино Тульской области Щёкино 2012 год Презентация цилиндра, пирамиды, конуса и шара
Введение Понятие объёма тела вводится по аналогии с понятием площади плоской фигуры. Из курса планиметрии известно, что каждый многоугольник имеет площадь, которая измеряется с помощью выбранной единицы измерения площадей. В качестве единицы измерения площадей обычно берут квадрат, сторона которого равна единице измерения отрезков. Аналогично будем считать, что каждое из рассматриваемых нам тел имеет объём, который можно измерить с помощью выбранной единицы измерения объёмов. За единицу измерения объёмов примем куб, ребро которого равно единице измерения отрезков. Куб с ребром 1 см называют кубическим сантиметром и обозначают см 3 . Аналогично определяются кубический метр (м 3), кубический миллиметр (мм 3) и т. д. Процедура измерения объёмов аналогична процедуре измерения площадей. При выбранной единице измерения объём каждого тела выражается поло -жительным числом, которое показывает, сколько единиц измерения объёмов и частей единицы содержится в данном теле. Ясно, что число, выражающее объём тела, зависит от выбора единицы измерения объёмов, и поэтому еди -ница измерения объёмов указывается после этого числа. Например, если в качестве единицы измерения объёмов взят 1 см 3 и при этом объём V некото -рого тела оказался равен 2, то пишут: V = 2 см 3 .
Если два тела равны, то каждое из них содержит столько же единиц измерения объёмов и её частей, сколько и другое тело, т. е. имеет следующее свойство объёмов: 1 0 . Равные тела имеют равные объёмы. Замечание Равенство двух фигур, в частности двух тел, в стереометрии определяется так же, как и в планиметрии два тела называются равными, если их совместить наложением. Примерами равных тел являются два прямоугольных параллелепипеда с соответственно равными измерениями, две прямые призмы с равными основаниями и равными высотами, две правильные пирамиды, у которых соответственно равны стороны оснований и высоты. В каждом из указанных случаев равенство двух тел можно доказать на основе аксиом наложения и равенства фигур. Рассмотрим ещё одно свойство объёмов, пусть тело составлено из нескольких тел. При этом мы предполагаем, что любые два из этих тел не имеют общих внутренних точек, но могут иметь общие граничные точки. Ясно, что объём всего тела складывается из объёмов составляющих его тел. Итак, 2 0 . Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Свойства 1 0 и 2 0 называют основными свойствами объёмов. Напомним, что аналогичными свойствами обладают длины отрезков и площади многоугольников. В дальнейшем на основе этих свойств мы выведем формулы для вычисления объёмов цилиндра, конуса, шара. Предварительно отметим одно следствие из свойств 1 0 и 2 0 . Рассмотрим куб, принятый за единицу измерения объёмов. Его ребро равно единице измерения отрезков. Разобьем каждое ребро этого куба на n равных частей (n – произвольное целое число) и проведём через точки разбиения плоскости прямые, перпендикулярные к этому ребру. Куб разобьётся на n 3 равных маленьких кубов с ребром 1/n . Так как сумма объёмов всех маленьких кубов равна объёму всего куба (свойство 2 0), т. е. равна 1, то объём каждого из маленьких кубов равен 1/n 3 (объёмы маленьких кубов равны друг другу по свойству 1 0). Итак, объём куба с ребром 1/n равен 1/n 3
Цилиндр Рассмотрим произвольную плос –кость и окружность L с центром O радиуса r , лежащую в этой плоскости. Через каждую точку окружности L проведём прямую, перпендикулярную к плоскости . Поверхность, образованная этими прямыми, называется цилиндрической поверх -ностью, а сами прямые – образующи -ми цилиндрической поверхности. Прямая, проходящая через точку O перпендикулярно к плоскости , называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны плоскости , то они параллельны друг другу. Рассмотрим теперь плоскость β , параллельную плоскости . Отрезки образующих, заключённые между плоскостями и β , параллельны и равны друг другу. По построению концы этих отрезков, расположенные в плоскости , заполняют окружность L . Концы же, расположенные в плоскости β , заполняют окружность L 1 с центром О 1 радиуса r , где О 1 – точка пересечения плоскости β с осью цилиндрической поверхности. Рис. 1 Основание цилиндра Основание цилиндра Ось цилиндра Боковая поверхность цилиндра Образующие цилиндра
Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β , получается из окружности L параллельным переносом на вектор ОО 1 . Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор ОО 1 окружность L перейдёт в равную ей окружность L 1 радиуса r центром в точке О 1 . Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L 1 называется цилиндром (Рис. 1). Круги называются основаниями цилиндра, отрезки образующих, заключённые между основаниями, – образующими цилиндра, а обрисованная ими часть цилиндрической поверхности – боковой поверхностью цилиндра. Ось цилиндрической поверхности называется осью цилиндра. Как уже отмечалось, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сто -рон. На рисунке 2 изображён цилиндр, по лученный вращением прямоугольника ABCD вокруг стороны AB . При этом боко -вая поверхность цилиндра образуется вращением стороны CD , а основания – вращением сторон BC и AD . Рис. 2
Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник (Рис. 3), две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым. Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, секущая плоскость (плоскость γ на рисунке 4) отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение. Рис. 3 Рис. 4
Замечание. На практике нередко встречаются предметы, которые имеют форму более сложных цилиндров. На рисунке 5.1 изображён цилиндр, каждое основание которого представляет собой фигуру, ограниченную частью параболы и отрезком. На рисунке 5.2 изображён цилиндр, основаниями которого являются круги, но образующие цилиндра не перпендикулярны к плоскостям оснований (наклонный цилиндр). Однако в дальнейшем мы будем рассматривать только такие цилиндры, которые были определены в этом пункте. Их называют иногда прямыми круговыми цилиндрами. Рис. 5.1 Рис. 5.2 Окружность Парабола
Объём цилиндра Говорят, что призма вписана в цилиндр, если основания вписаны в основания цилиндра (Рис. 6), и призма описана около цилиндра, если её основания описаны около оснований цилиндра (Рис. 7). Ясно, что высота любой призмы, вписанной в цилиндр или описанной около него, равна высоте самого цилиндра. Рис. 6 Рис. 7
Будем неограниченно увеличивать число n . При этом радиус r n цилиндра Р n стремится к радиусу r цилиндра Р: r n = r cos 180 / n при n → ∞ . Поэтому объём цилиндра Р n стремится к объёму цилиндра Р: . Из неравенства (1) следует, что и. Но. Таким образом: V = r 2 h . (2) Обозначив площадь r 2 основания цилиндра буквой S , из формулы (2) получим: V = S · h . Теорема доказана. Теорема Объём цилиндра равен произведению площади основания на высоту. Доказательство Впишем в данный цилиндр Р радиуса r и высоты h правильную n - угольную призму F n , а в эту призму впишем цилиндр Р n (Рис. 8). Обозначим через V и V n объёмы цилиндров Р и Р n , через радиус цилиндра r n. Так как объём призмы F n равен S n · h , где S n – площадь основания призмы, а цилиндр Р содержит призму F n , которая, в свою очередь, содержит цилиндр Р n , то V n
Площадь цилиндра На рисунке 9.1 изображён цилиндр. Представим себе, что его боковую поверхность разрезали по образующей AB и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости (Рис 9.2). В результате в плоскости получится прямоугольник ABA ´ B ´ . Стороны AB и A ´ B ´ прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей AB . Этот прямоугольник называется развёрткой боковой поверхности цилиндра. Основание AA ´ прямоугольника является развёрткой окружности основания цилиндра, а высота AB – образующей цилиндра, поэтому AA ´ = 2 r , AB = h , где r – радиус цилиндра, h – его высота. За площадь боковой поверхности цилиндра принимается площадь её развёртки. Так как площадь прямоугольника ABA ´ B ´ равна AA ´· AB = 2 r h , то для вычисления площади S бок боковой поверхности цилиндра радиуса r и высоты h получается формула: S бок = 2 r h . Итак, площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра. Рис. 9 .1 Рис. 9 . 2
Пирамида Рассмотрим многоугольник А 1 A 2 …A n и точку P , не лежащую в плоскости этого многоугольника. Соединив точку P отрезками с вершинами многоугольника, получим n треугольников (Рис 10): P А 1 A 2 , P А 2 A 3 ,…, PA n А 1 . (1) Многогранник, составленный из n – угольника А 1 A 2 …A n и n треугольников (1), называется пирамидой. Многоугольник А 1 A 2 …A n называется основанием, а треугольники (1) – боковыми гранями пирамиды. Точка P называется вершиной пирамиды, а отрезки P А 1 ,P А 2 ,…,PA n – её боковыми рёбрами. Пирамиду с основанием А 1 A 2 …A n и вершиной P обозначают так: P А 1 A 2 …A n – и называют n - угольной пирамидой. На рисунке 11 изображены четырёхугольная и шестиугольная пирамиды. Ясно, что треугольная пирамида – это тетраэдр. Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды. На рисунке 10 отрезок PH является высотой пирамиды. Площадью полной поверхности пирамиды называется сумма площадей всех её граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды – сумма площадей её боковых граней. Очевидно, S полн. = S бок + S осн.
Рис. 11 Рис. 10
Правильная пирамида Пирамида называется правильной, если ее основание - правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой (Рис. 12). Докажем, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.




Выпуклый многогранник Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками. В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360 градусов.






Элементы призмы – Основание призмы 2 – Высота 3 – Боковая грань
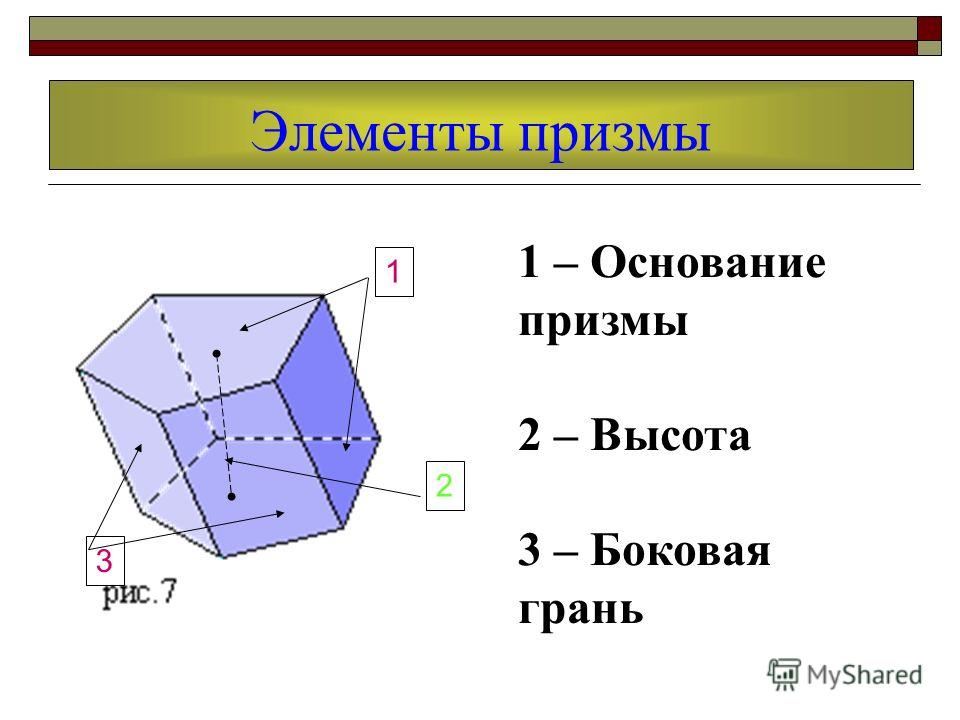


Элементы пирамиды высота пирамиды 2-боковая грань пирамиды 3-основание пирамиды




![]()



Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине равна 324 градусов. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер.





ЦИЛИНДР Цилиндром называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра (3), а отрезки – его образующими (4). Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. Радиусом цилиндра называется радиус его основания(1). Высотой цилиндра называется расстояние между плоскостями оснований (2). Осью цилиндра называется прямая, проходящая через центры оснований. 4 5

КОНУС Конусом называется тело, которое состоит из круга – основания конуса(5), точки, не лежащей в плоскости этого круга – вершины конуса(2), и всех отрезков, соединяющих вершину конуса с точками основания – образующих конуса. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания(1). Осью конуса называется прямая, содержащая его высоту. Полная поверхность конуса состоит из его основания(5) и боковой поверхности (3). Радиусом конуса – радиус его основания.
СФЕРА И ШАР Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (3). Данная точка называется центром сферы, а данное расстояние- радиусом сферы (1). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Плоскость, проходящая через центр шара, называется диаметральной плоскостью (2). Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью. 3


· Шар называется вписанным в многогранник, а многогранник описанным около шара, если поверхность шара касается всех граней многогранник
· Шар называется описанным около многогранника, а многогранник –вписанным в шар, если поверхность шара проходит через все вершины многогранника

· Шар называется вписанным в цилиндр, а цилиндр – описанным около шара, если поверхность шара касается оснований цилиндра и всех его образующих.

· Шар называется вписанным в конус, а конус – описанным около шара, если поверхность шара касается основания конуса и всех его образующих.
· Шар называется вписанным вусеченный конус, аусеченный конус – описанным около шара, если поверхность шара касается оснований конуса и всех его образующих.
· Шар называется описанным около цилиндра, если окружности оснований цилиндра принадлежат поверхности шара.
· Шар называется описанным около конуса, если окружностьоснования и вершина конуса принадлежат поверхности шара.

· Шар называется описанным около усеченного конуса, если окружностиоснований конуса принадлежат поверхности шара.
Положение центра шара вписанного в многогранник
· Центр шара вписанного в многогранник – это точка пересечения биссекторных плоскостей всех двухгранных углов многогранника. Он может быть расположен только внутри многогранника.
Положение центра шара описанного около многогранника
· Центр шара, описанного около многогранника, это точки пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен, на поверхности и вне многогранника.
Положение центра шара вписанного в пирамиду
Если
боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую
пирамиду можно вписать шар (условие достаточное, но не необходимое). Центр шара
есть точка пересечения высоты пирамиды с биссектрисой линейного угла любого
двугранного угла при основании пирамиды, одной из сторон
которого служит высота боковой грани, проведенная из вершby пирамиды. В правильную пирамиду всегда можно вписать шар.
Положение центра шара вписанного в пирамиду
Около пирамиды можно описать шар тогда и только тогда, когда около ее основания можно описать окружность. В частности, шар можно описать около треугольной пирамиды; около любой правильной пирамиды; около четырехугольной пирамиды, у которой сумма противоположных углов основания равна 180°. Центр шара, описанного около пирамиды, есть точка пересечения пря мой, перпендикулярной основанию пирамиды и проходящей че рез центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру и проведенной через середину этого ребра.
Если боковые ребра пирамиды равны между собой (или одинаково наклонены к плоскости основания), то около такой пирамиды можно описать шар. Центр шара в этом случае находится в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.
Шар и призма
· Шар, вписанный в призму, должен касаться всех ее граней. В призму можно вписать шар тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, а высота призмы равна диаметру окружности, вписанной в это перпендикулярное сечение. Если при этом призма прямая, то ортогональная проекция шара на плоскость основания призмы является кругом, вписанным в многоугольник основания. Для наклонной призмы проекция шара на плоскость основания является кругом, выходящим за пределы основания. Но в любом случае высота призмы равна диаметру вписанного шара.

·
Описать шар
около призмы можно тогда и только тогда, когда призма прямая и около ее
основания можно описать окружность. В этом случае многоугольники оснований
призмы являются вписанными в некоторое сечение шара, не проходящее через его
центр, а все вершины призмы лежат на поверхности шара.
Конус и призма
Прямой круговой конус вписан в призму, если его вершина лежит на верхнем оснований призмы, а его основание есть круг, вписанный в многоугольник нижнего основания призмы. В этом случае многоугольник основания призмы должен быть таким, чтобы в него можно было вписать окружность. Прямая, перпендикулярная к нижнему основанию и проходящая через центр круга, вписанного в многоугольник оснований, должна пересекать верхнее основание, так как эта прямая является осью конуса. Высота конуса равна высоте призмы.
Прямой круговой конус описан около призмы, если все вершины верхнего основания призмы лежат на боковой поверхности конуса, а нижнее основание призмы лежит в плоскости основания конуса. В этом случае основанием призмы служит многоугольник, вокруг которого можно описать окружность, но нижнее основание призмы не вписано в основание конуса.

Цилиндр и призма
Цилиндр может быть вписан в прямую призму, основаниями которой являются многоугольники, в которые можно вписать окружность.

Цилиндр может быть описан около прямой призмы, основанием которой являются многоугольники, около которых можно описать окружность. Высота призмы совпадает с высотой цилиндра.

Конус и пирамида
В правильную пирамиду можно вписать конус и описать около нее конус. При этом вершина конуса совпадает с вершиной пирамиды, основание конуса лежит в плоскости основания пирамиды и является вписанным или описанным кругом соответственно.
Цилиндр и пирамида
В пирамиду можно вписать прямой круговой цилиндр. При этом окружность одного из оснований цилиндра касается всех боковых граней пирамиды, а другое основание цилиндра лежит в плоскости основания пирамиды, но не является вписанным в многоугольник основания, а находится внутри его.
Пирамида вписана в цилиндр, если ее основание лежит в плоскости одного из оснований цилиндра и является многоугольником, вписанным в окружность основания цилиндра, а вершина пирамиды находится в плоскости другого основания цилиндра.
3.2.3. геометрические объекты:
пирамида, призма, цилиндр, конус и другие
Пирамида
–
это многогранник, одна грань
которого многоугольник, а остальные грани –
треугольники с общей вершиной (рисунок 3.54). Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина ее отсекается плоскостью.
Многогранником называется геометрический объект, ограниченный совокупностью плоских многоугольников, у которых каждая сторона одного является одновременно стороной другого (но только одного).
Построение графического отображения многогранника сводится к построению проекций его вершин и ребер. Кратко охарактеризуем геометрические свойства некоторых многогранников и выполним их проекции.
Призма – многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани – параллелограммы (рисунок 3.55). Название призмы зависит от того, какой многоугольник лежит в ее основании: если треугольник, то призма – треугольная, если четырехугольник, то – четырехугольная и т. д. Если основанием призмы является параллелограмм, то такая призма – параллелепипед. Призма называется прямой, если ее ребра перпендикулярны плоскости основания. Прямоугольный параллелепипед, все ребра которого конгруэнтны между собой, называется кубом.
|
Призматоид
–
многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой
треугольники и трапеции, вершины которых служат вершинами и многоугольников оснований (рисунок 3.56).
Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными . Углы при вершинах такого многогранника равны между собой. Существует пять типов правильных многогранников, свойства которых описал более двух тысяч лет назад древнегреческий философ Платон, чем и объясняется их общее название. Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.
Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками. Это правильная треугольная пирамида.
Гексаэдр – правильный шестигранник. Это куб, ограниченный шестью равными квадратами.
Октаэдр – правильный восьмигранник, ограниченный восемью равносторонними и равными между собой треугольниками, соединенными по четыре у каждой вершины (рисунок 3.57).
Икосаэдр – правильный двадцатигранник, ограниченный двадцатью равносторонними и равными треугольниками, соединенными по пять у каждой вершины (рисунок 3.58).
Додекаэдр – правильный двенадцатигранник, ограниченный двенадцатью правильными и равными пятиугольниками, соединенными по три у каждой вершины (рисунок 3.59).
|
Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Достраивая пересечения продолжений граней Платоновых тел, можно получать звездчатые многогранники. В качестве примера рассмотрим две наиболее простые звездчатые формы.
Звездчатый октаэдр. Восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые «куски», внешние по отношению к октаэдру. Это малые тетраэдры, основания которых совпадают с гранями октаэдра (рисунок 3.60). Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Такой звездчатый многоугольник в 1619 г. описал Кеплер и назвал его stella ostangula – восьмиугольная звезда.
Малый звездчатый додекаэдр – звездчатый додекаэдр первого продолжения. Он образован продолжением граней правильного выпуклого додекаэдра до их пересечения. Каждая грань выпуклого додекаэдра при продолжении сторон образует правильный звездчатый пятиугольник (рисунок 3.61). Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые «куски», внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра.
Цилиндр – геометрический объект, ограниченный цилиндрической поверхностью и двумя плоскостями, называемыми основаниями. В зависимости от угла наклона образующих цилиндрической поверхности к основанию различают прямой цилиндр (угол наклона 90°) и наклонный (рисунок 3.62).
|
Конус – геометрический объект, ограниченный конической поверхностью и плоскостью, называемой основанием или двумя плоскостями (усеченный конус). Конус может быть прямым (рисунок 3.63) или наклонным.
Шар – геометрический объект, образованный вращением круга вокруг его диаметра (рисунок 3.64). При сжатии или растяжении шар преобразуется в эллипсоид , который может быть получен вращением эллипса вокруг одной из осей: если вращение происходит вокруг большой оси, то эллипсоид называется вытянутым ; если вокруг малой – сжатым, или сфероидом (рисунок 3.65).
Тор – геометрический объект, образованный при вращении круга вокруг оси, не проходящей через его центр (рисунок 3.66).
|
|
|








